Find the center, transverse axis, vertices, foci, and asymptotes for the hyperbolaCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andAnswer by Fombitz () ( Show Source ) You can put this solution on YOUR website!

Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy
(x-2)^2+(y+1)^2=9 graph
(x-2)^2+(y+1)^2=9 graph-A sphere is the graph of an equation of the form x 2 y 2 z 2 = p 2 for some real number p The radius of the sphere is p (see the figure below) Ellipsoids are the graphs of equations of the form ax 2 by 2 cz 2 = p 2, where a, b, and c are all positiveFormula for love X^2(ysqrt(x^2))^2=1 (wolframalphacom) 2 points by carusen on Feb 14, 11 hide past favorite 41 comments ck2 on Feb 14, 11



Mrs Rivas Ppt Download
How To Given the standard form of an equation for an ellipse centered at (0,0) ( 0, 0), sketch the graph Use the standard forms of the equations of an ellipse to determine the major axis, vertices, covertices, and foci If the equation is in the form x2 a2 y2 b2 = 1 x 2 a 2 y 2 b 2 = 1May 03, 14 · x 2 /4 y 2 /9 = 1 The equation is y 2 /9 x 2 /4 = 1 The standard form of the equation of an ellipse center (h, k) with major and minor axes of lengths 2 2 (y k ) 2 /b 2 = 1 or (x h) 2 /b 2 (y k) 2 /a 2 = 1The vertices and foci lie on the major axis, a and c units, respectively, from the center (h, k ) and the relation between a, bCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
I am already using it and I only can plot in 2 dimensional graph Can someone help me with this problem?Graph {eq}(x 2)^2 (y 1)^2 = 9 {/eq} Circles A circle is a two dimensional relationship for which every point is equally distant from the point in the centerEvery line through the center is a line of symmetry The yaxis and the xaxis are lines of symmetry ( my choice) Every line through the center is a line of symmetry The yaxis and the xaxis are lines of symmetry 2 Graph
Substitute x=2y into x^2y^2=9, to give (2y)^2y^2=9 Expand the brackets using FOIL to give 44yy^2y^2=9 By grouping like terms together get 2y^24y5=0 Because the question asks for the answer in 2dp, you know to use the quadratic formula, so substitute into the given formula where a=2, b=4 and c=5 (dont forget the minus sign!)It's the equation of sphere The general equation of sphere looks like math(xx_0)^2(yy_0)^2(zz_0)^2=a^2/math Wheremath (x_0,y_0,z_0)/math is the centre of the circle and matha /math is the radious of the circle It's graph looksThat's a circle Compare mathx^2y^22x=0/math with the general equation of a circle mathx^2y^22gx2fyc=0/math and write down the values of the constants


Pplato Basic Mathematics Quadratic Functions And Their Graphs



Mrs Rivas Ppt Download
Plotting graphics3d Share Improve this question Follow asked Nov 29 '15 at 533 user userThe graph of mathx^2(y\sqrt3{x^2})^2=1/math is very interesting and is show below using desmosCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
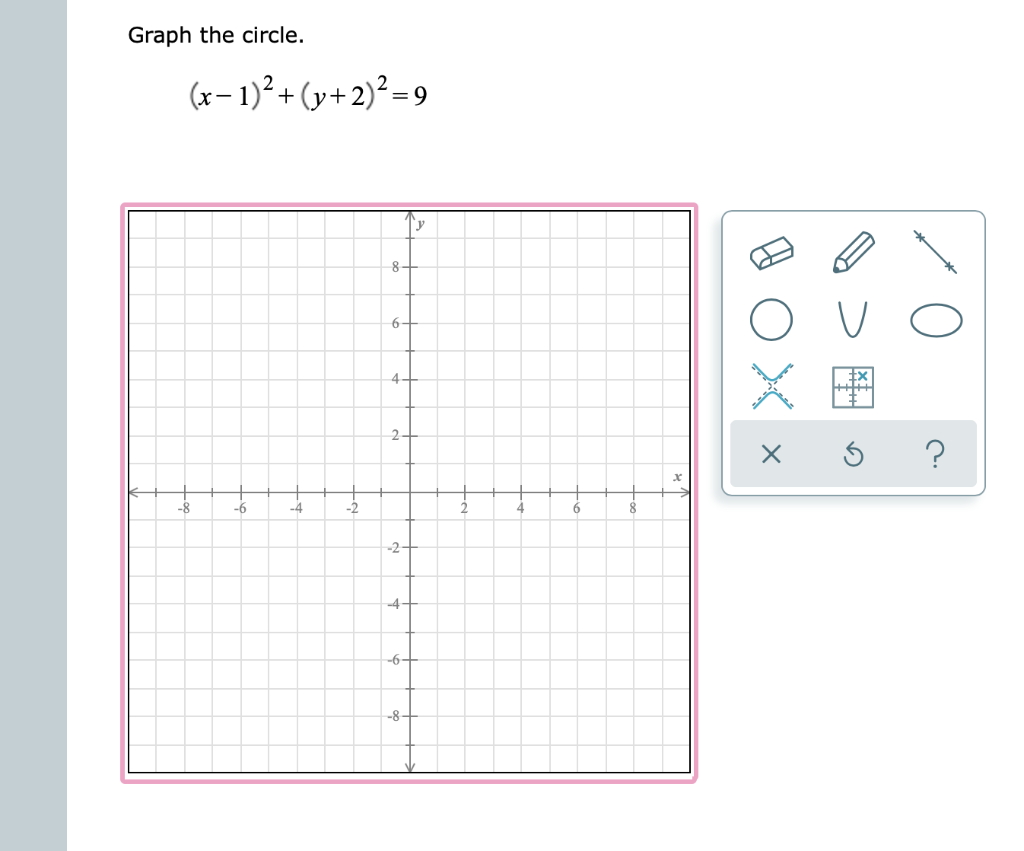


Solved Graph The Circle X 1 2 Y 2 9 O Hxow X 5 Chegg Com



11 Maths Adv 19 Mr Harris Com
Popular Problems Algebra Graph x^2y^2=9 x2 y2 = 9 x 2 y 2 = 9 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yPreAlgebra Graph x^2y^2=1 x2 − y2 = −1 x 2 y 2 = 1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive − x 2 y 2 = 1 x 2 y 2 = 1 Simplify each term in the equation in order to set the right side equal to 1 1Apr 04, 10 · Favorite Answer (x^ (2))/ (36)y^ (2)=1 Simplify each term in the equation in order to set the righthand side equal to 1 The standard form of an ellipse or hyperbola requires the righthand side of the equation be 1 (x^ (2))/ (36) (y^ (2))/ (1)=1 This is the form of a hyperbola Use this form to determine the values used to find vertices



画像をダウンロード 2x Y2 9x Y 5 中学 地理 プリント



Draw The Graph Of 2x Y 1 0 And 2x Y 9 On The Same Graph Use 2 Cm 1 Unit On Both Axes Write Down The
Y2 9 − x2 1 = 1 This is the equation of an updown hyperbola The general equation is (y− k)2 a2 − (x −h)2 b2 = 1 The center is (h, k) = (0,0) The vertices are (h, k± a), A = (0,3) and A' = (0, −3) The slope of the asymptotes are ± a b = ±3 The equations of the asymptotes are y = 3x and y = − 3x To determine the foci, we need c, c2 = a2 b2Algebra Graph x^2 (y2)^2=4 x2 (y − 2)2 = 4 x 2 ( y 2) 2 = 4 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h hThe graph is attached below Stepbystep explanation y – 1 = 2 (x – 2) y1 = 2x 4 add 1 on both sides y = 2x 3 To graph the given equation we make a table Plug in some number for x and find out the value of y x y = 2x3
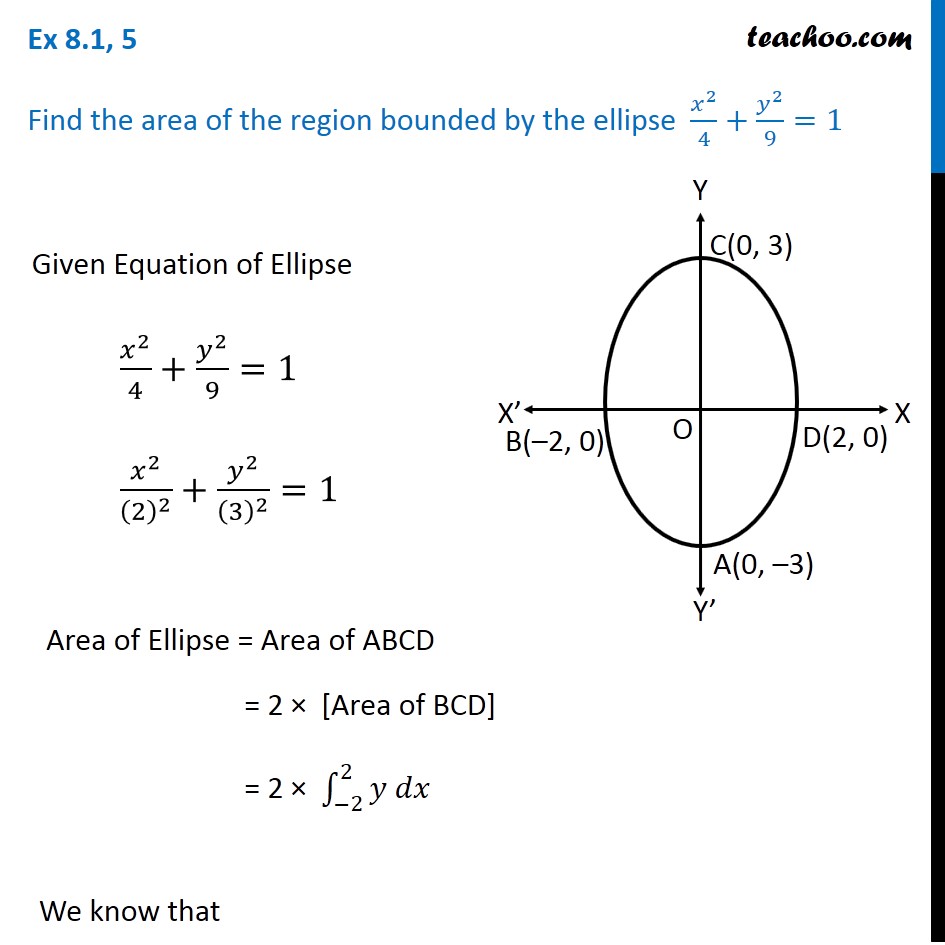


Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12



Answered 0 2 2 2 2 2 2 E D F 2 Bartleby
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolve for y Subtract x^ {2} from both sides of the equation Subtract x 2 from both sides of the equation Subtracting x^ {2} from itself leaves 0 Subtracting x 2 from itself leaves 0 Take the square root of both sides of the equation Take the square root of both sides of the equation Subtract \sqrt 3 {x} from both sides of the equationA log–log plot of y = x (blue), y = x2 (green), and y = x3 (red) Note the logarithmic scale markings on each of the axes, and that the log x and log y axes (where the logarithms are 0) are where x and y themselves are 1 In science and engineering, a log–log graph or log–log plot is a twodimensional graph of numerical data that uses


Graph Of Y X 2 3 X Geogebra
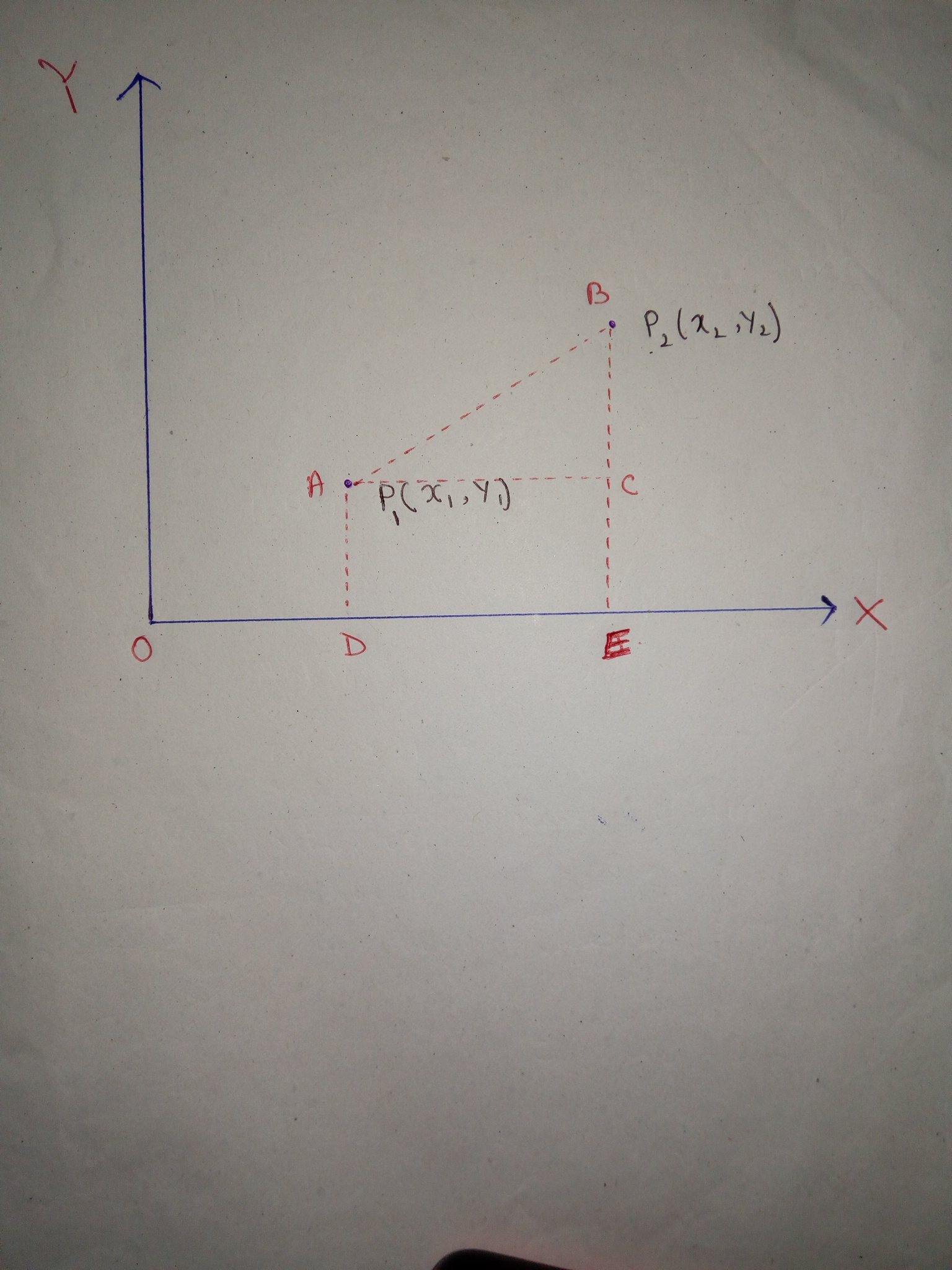


Distance Formula Algebra Socratic
Weekly Subscription $299 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledY = x2 y = x 2 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side x2=y x 2 = y Subtract 2 from both sides Subtract 2 from both sides x=y2Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be moved down by 2 units So we just take our first curve and move it down 2 units Our new curve's vertex is at −2 on the yaxis



Y 1 2 Y 1 2 Y 1 Y X 2 X Y Y 1 2 Y 3 1 3 Ppt Download



Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy
How do you graph y=x2Video instruction on how to graph the equation y=x2 how do you graph y=x2Video instruction on how to graph the equation y=x2Graph of x^2y^2=9 Below you can find the full step by step solution for you problem We hope it will be very helpful for you and it will help you to understand the solving process If it's not what You are looking for, type in into the box below your own function and let us find the graph of it The graph of x^2y^2=9 represents a graph of aFind the x and y intercepts To find the xintercept, set y=0 and solve for x (5,0) and (5,0) To find the yintercept, set
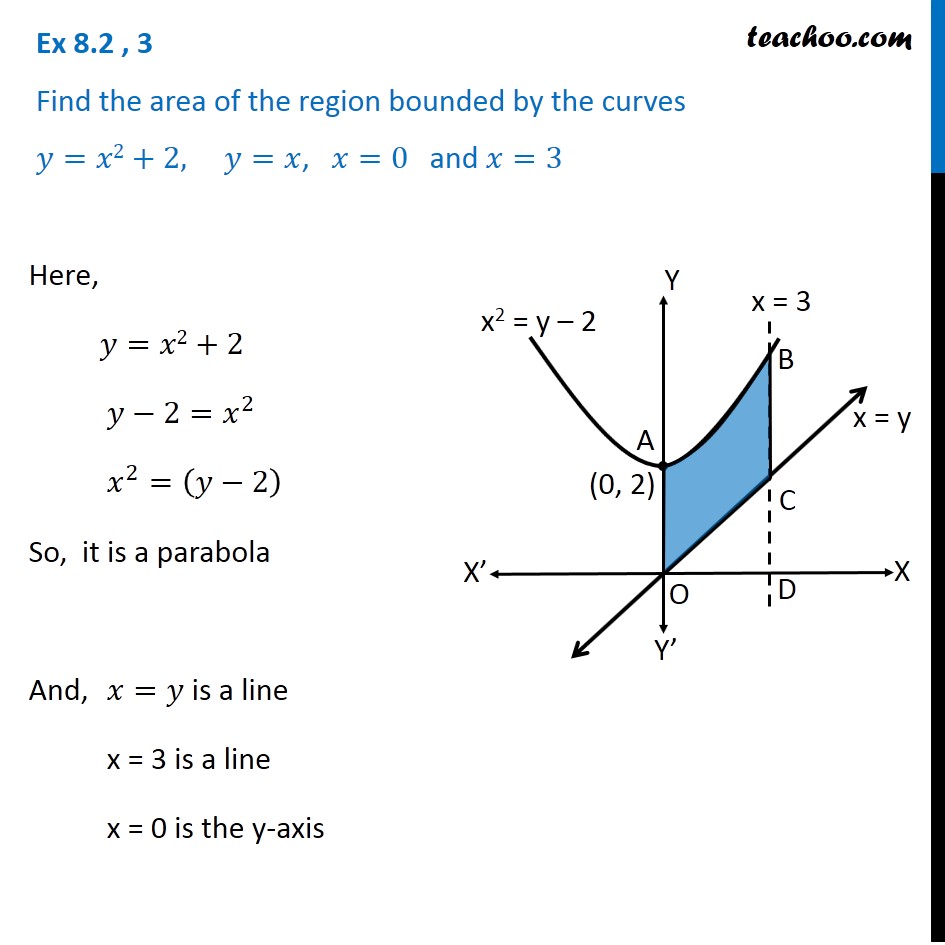


Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3



Vertices Direction Of A Hyperbola Example 2 Video Khan Academy
All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}8xy1=0 x 2 8 x − y − 1 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 8 for b, andSuppose that \frac {x^2} {\sqrt {x^2y^2}}=f (x)g (y) for some functions f and g Then f (1)g (1)=\frac {1} {\sqrt {2}}, It cannot be done Suppose to the contrary that it can be done We will derive a contradiction Suppose that x2y2Steps to graph x^2 y^2 = 4



Ppt Circles In The Coordinate Plane Powerpoint Presentation Free Download Id


Graphing A Line Given Point And Slope Video Khan Academy
Plot x^2y^2x Extended Keyboard;Jul 07, 15 · Step 3 Find the vertical asymptotes Set the denominator equal to zero and solve for x x^2 9 = 0 x^2 = 9 x = ±3 There are vertical asymptotes at x = 3 and x = 3 Step 4 Find the horizontal asymptote Both equations are of the second order, so we divide the coefficients of the x^2 terms 1/1 = 1 The horizontal asymptote is at y=1 Step 5Jul 07, 18 · A circle with a radius of 3, and its center located at (4,1) Given (x4)^2(y1)^2=9 Notice that the equation for a circle is given by (xa)^2(yb)^2=r^2 where (a,b) are the coordinates of the circle's center r is the radius of the circle Here, we get (a,b)=(4,1), and 9=3^2
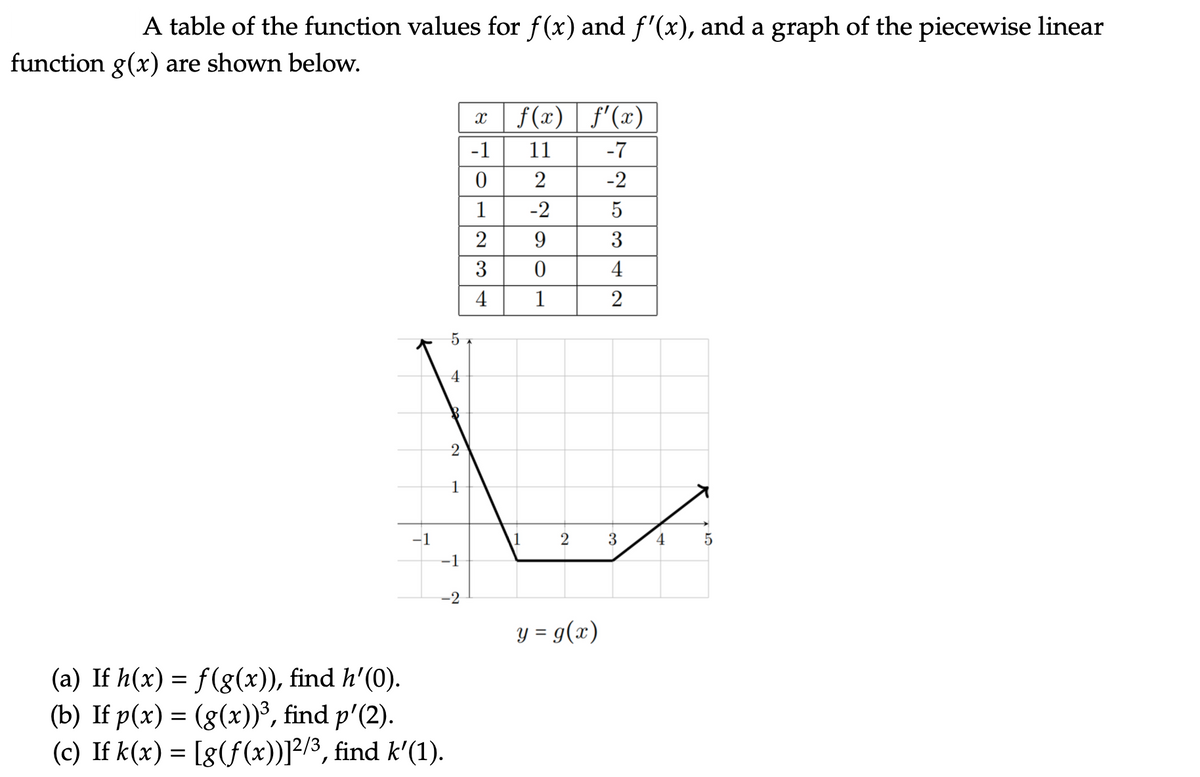


Answered A Table Of The Function Values For F X Bartleby
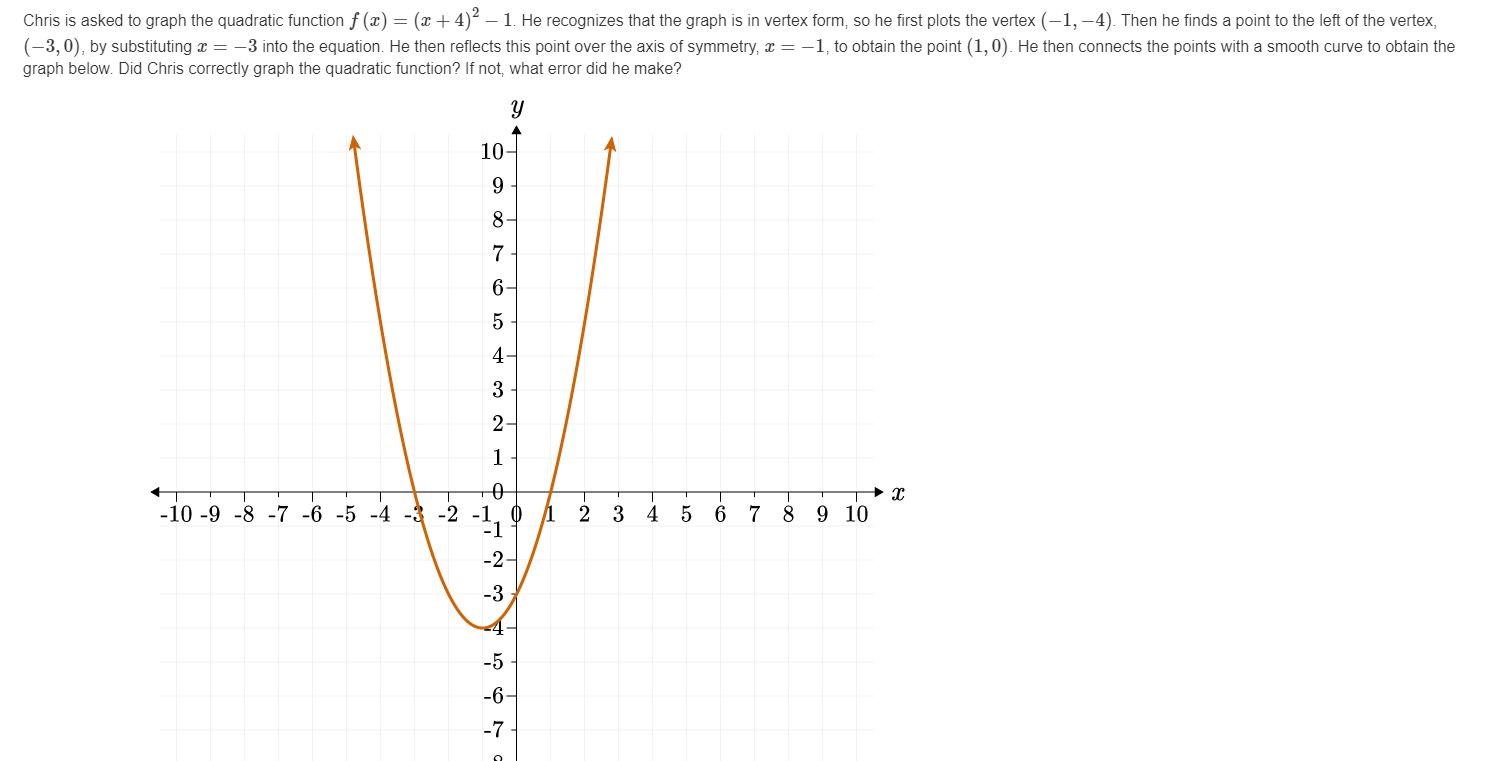


Solved Chris Is Asked To Graph The Quadratic Function F Chegg Com
Click here to see ALL problems on Quadraticrelationsandconicsections Question x^2/25y^2/16=1 How to graph that ellipse?Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled1 Graph x2 y2 = 9 What are its lines of symmetry?



X 2 Y 2 9 Graph Page 1 Line 17qq Com



Parent Functions And Their Graphs Video Lessons Examples And Solutions
Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledGraph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yList all of the vertical asymptotes x = −1,1 x = 1, 1 Consider the rational function R(x) = axn bxm R ( x) = a x n b x m where n n is the degree of the numerator and m m is the degree of the denominator 1 If n < m n < m, then the xaxis, y = 0 y = 0, is the horizontal asymptote 2



X 2 Y 2 9 Graph Page 1 Line 17qq Com



Graph X 2 Y 2 4 Youtube
Feb 28, 16 · Explanation This is the equation of a circle with its centre at the origin Think of the axis as the sides of a triangle with the Hypotenuse being the line from the centre to the point on the circle By using Pythagoras you would end up with the equation given where the 4 is in fact r2 To obtain the plot points manipulate the equation as below Given x2 y2 = r2 → x2 y2 = 4Click here to see ALL problems on Quadraticrelationsandconicsections Question graph the ellipse and its foci x^2/9 y^2/4=1 Answer by lwsshak3 () ( Show Source ) You can put this solution on YOUR website!Sep 12, 10 · The graph is indeed an ellipse x^2/64 y^2/9 = 1 (multiply each term by 64*9 to clear the fractions) 9x^2 64y^2 = 576 64y^2 = 9x^2 576 y^2 = (9x^2)/64 576/64 y^2 = (9/64)x^2 9 y = /sqrt (9/64)x^2 9 Without using a graphing calculator, you need the x and yintercepts xintercepts are where the y coordinate is = 0, so



Rectangular Coordinate System



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
To zoom, use the zoom slider To the left zooms in, to the right zooms out When you let go of the slider it goes back to the middle so you can zoom more You can clickanddrag to move the graph around If you just clickandrelease (without moving), then the spot you clicked on will be the new center To reset the zoom to the original clickReplace g (x) = y to get x^2 y^2 = 9 We know For a function g(x) = 9− x2 , we can square it to find g2(x) = 9− x2 Adding x2 to both sides, we now have g2(x)x2 = 9 Replace g(x) = y to get x2 y2 = 9 We know Integrate \sqrt {1x^2} on x=1 to 1How to plot 3 dimensional graph for x^2 y^2 = 1?



Graphs Of Linear Functions Precalculus I



Bellwork Graph Each Line 1 3x Y 6 2 Y 1 2 X 3 Y Ppt Video Online Download
Jul 26, 18 · Explanation Given y = x2 − 9 is a quadratic equation in standard form y = ax2 bx c, where a = 1, b = 0, and c = −9 To graph a quadratic equation in standard form, you need the vertex, yintercept, xintercepts (if real), and one or two additional points Vertex maximum or minimum point (x,y) of the parabolaGraph the ellipse and its foci x^2/9 y^2/4=1 standard forms of ellipse (xh)^2/a^2 (yk)^2/b^2=1 (horizontalTrigonometry Graph (x2)^2 (y1)^2=9 (x 2)2 (y 1)2 = 9 ( x 2) 2 ( y 1) 2 = 9 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form
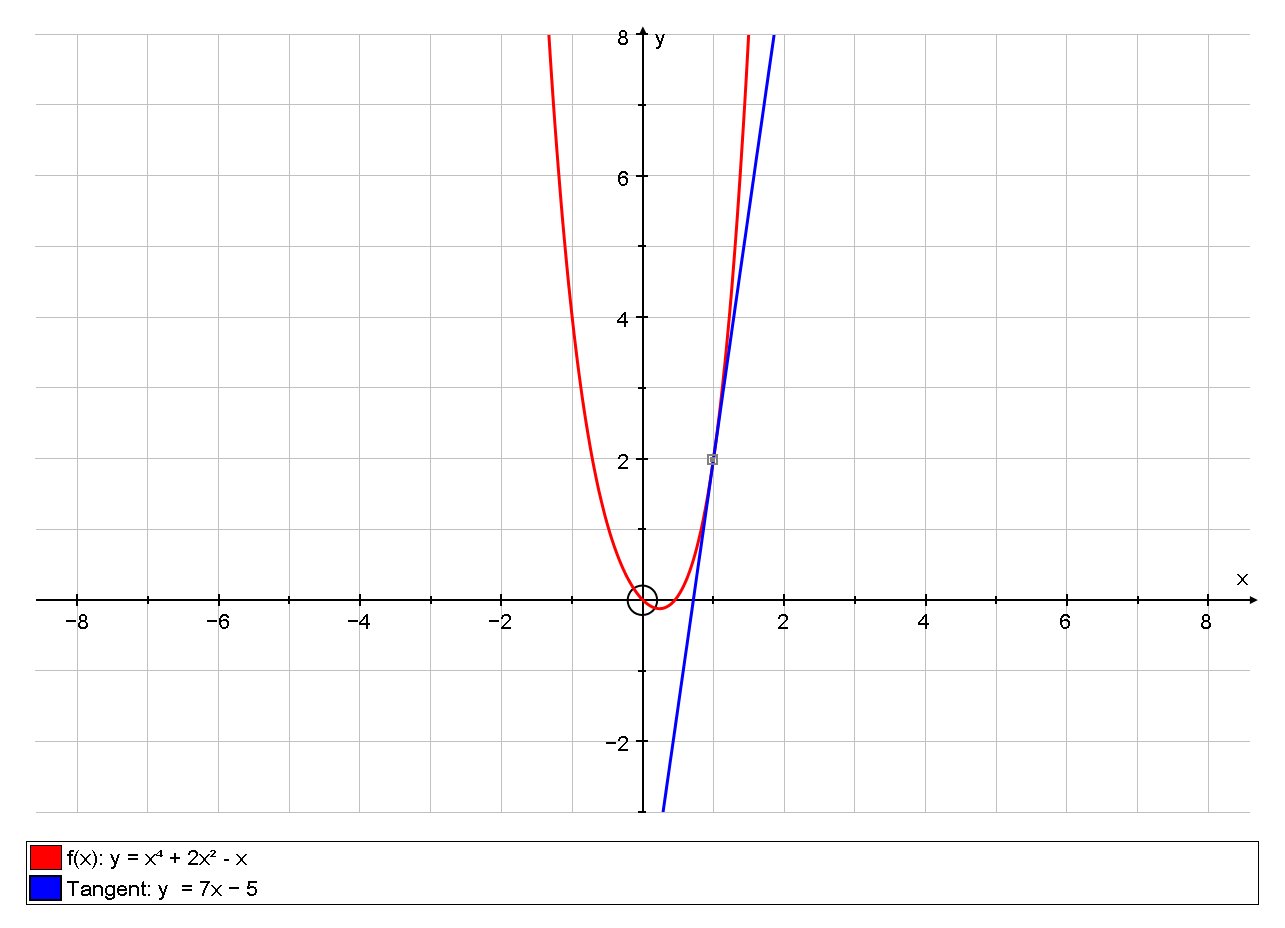


How Do You Find The Equation Of The Tangent Line To The Curve Y X 4 2x 2 X At 1 2 Socratic
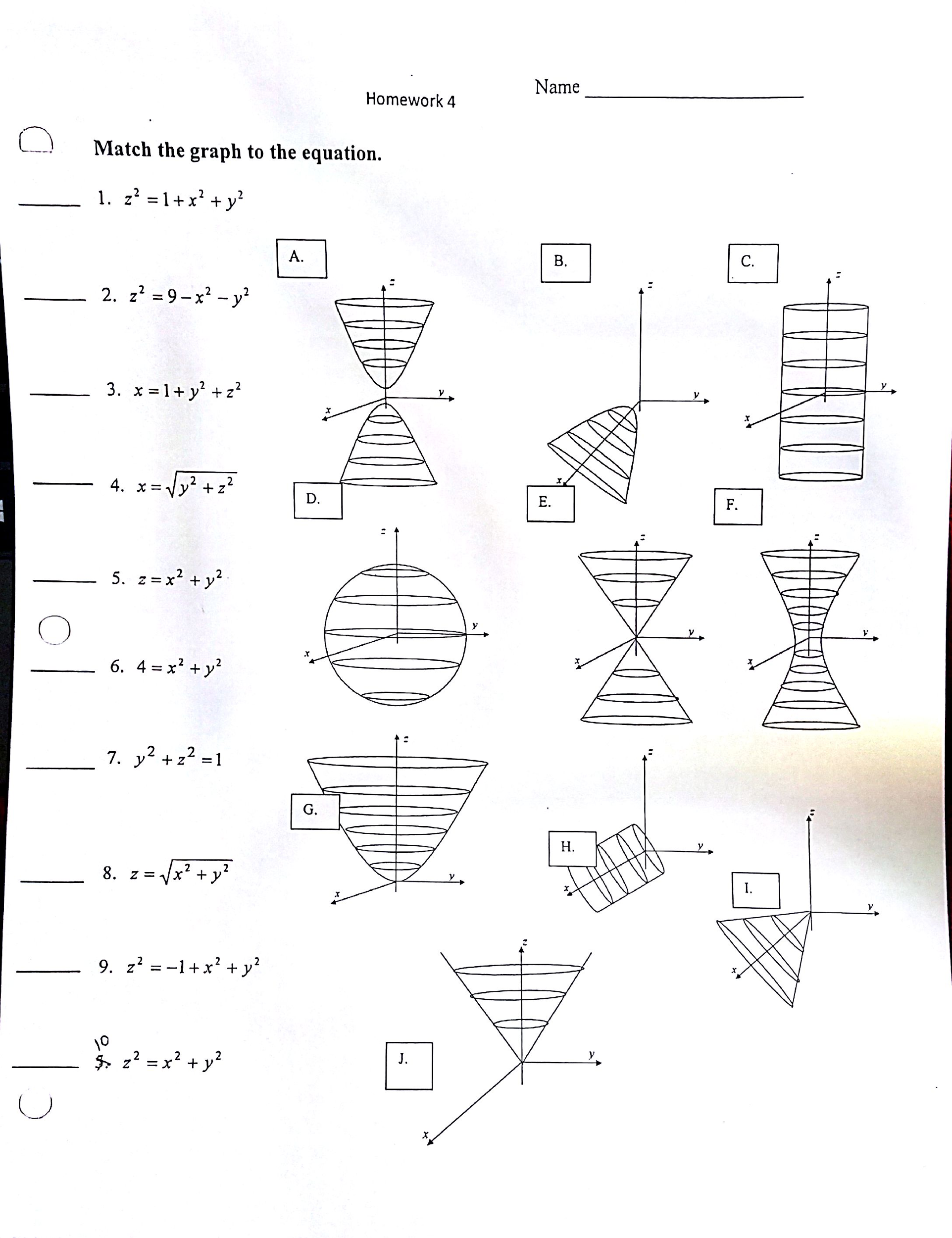


Solved Match The Graph To The Equation X 2 1 X 2 Y Chegg Com
1 2 plane is the hyperbola y2 9 z2 4 = 1, shown below For problems 1415, sketch the indicated region 14 The region bounded below by z = p x 2 y and bounded above by z = 2 x2 y2 15 The region bounded below by 2z = x2 y2 and bounded above by z = y 7
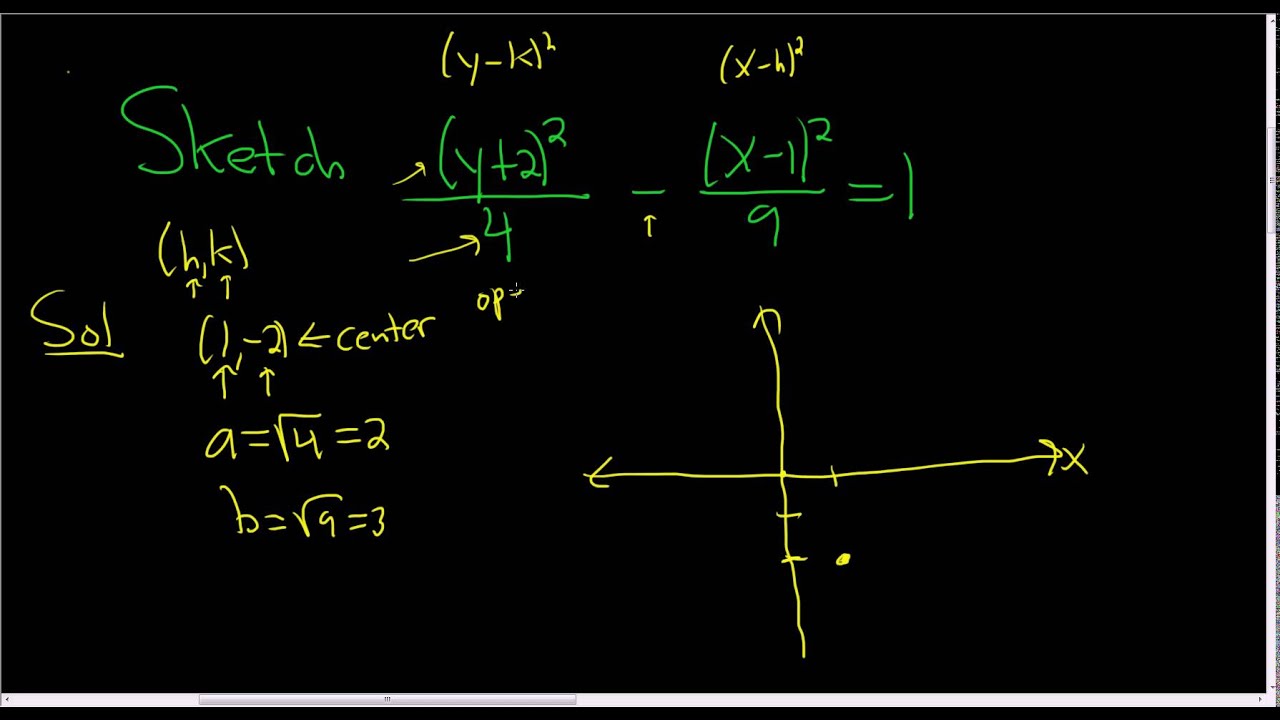


Graph The Hyperbola Y 2 2 4 X 1 2 9 1 Youtube



Section 11 6 Conic Sections Ppt Download



Text Q Find The Area Enclosed By The Curves Y 2 X 2 9 Text And Left Left X 2 Y Left X Right Right Right 1 Mathematics Stack Exchange



Complete Quadratic Graph Tables Worksheet Edplace



Use The Drawing Tool S To Form The Correct Answer On The Provided Graph Plot The X Intercept S Brainly Com



If P Is A Point On The Hyperbola X 2 16 Y 2 9 1 And Q Be The Focus Of The Parabola Y 2 8x Youtube
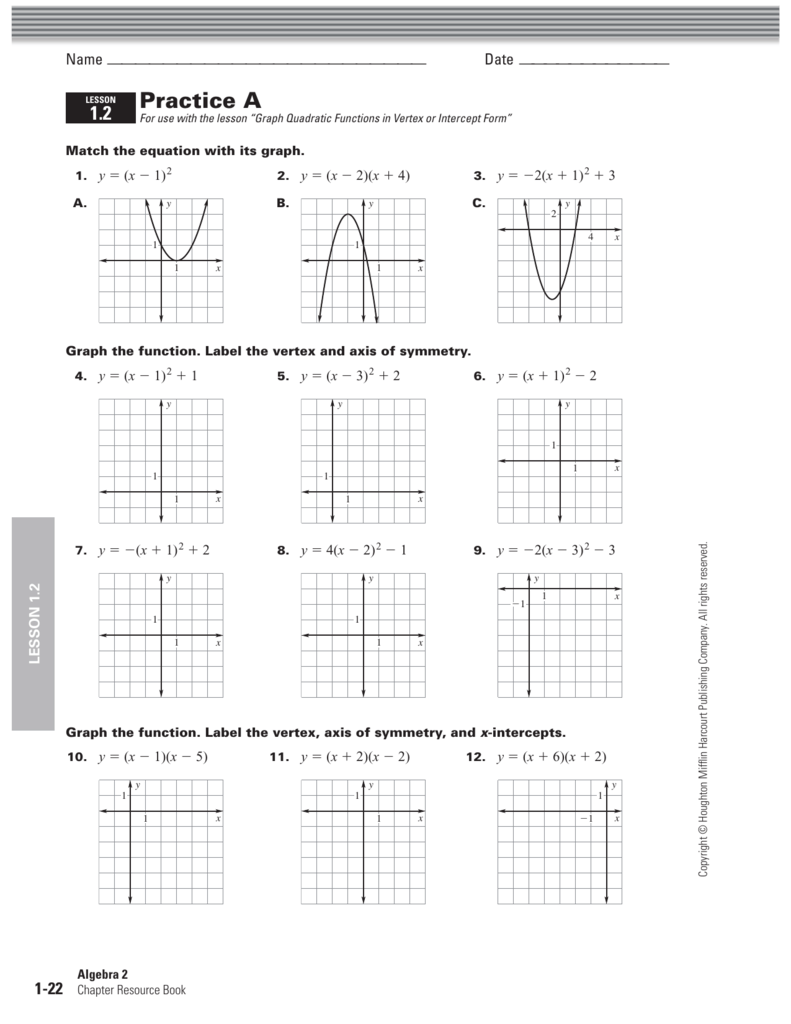


Practice 1 2 Graphing In Vertex Form And Intercept Form



X 2 Y 2 9 Graph Page 1 Line 17qq Com



Write The Equation Of The Ellipse Shown In The Graph A X 1 2 4 Y 2 2 9 1b X 1 2 9 Brainly Com
/1000px-Parabola_features-58fc9dfd5f9b581d595b886e.png)


How To Find Quadratic Line Of Symmetry



Graphs Of Linear Functions Precalculus I



Circles
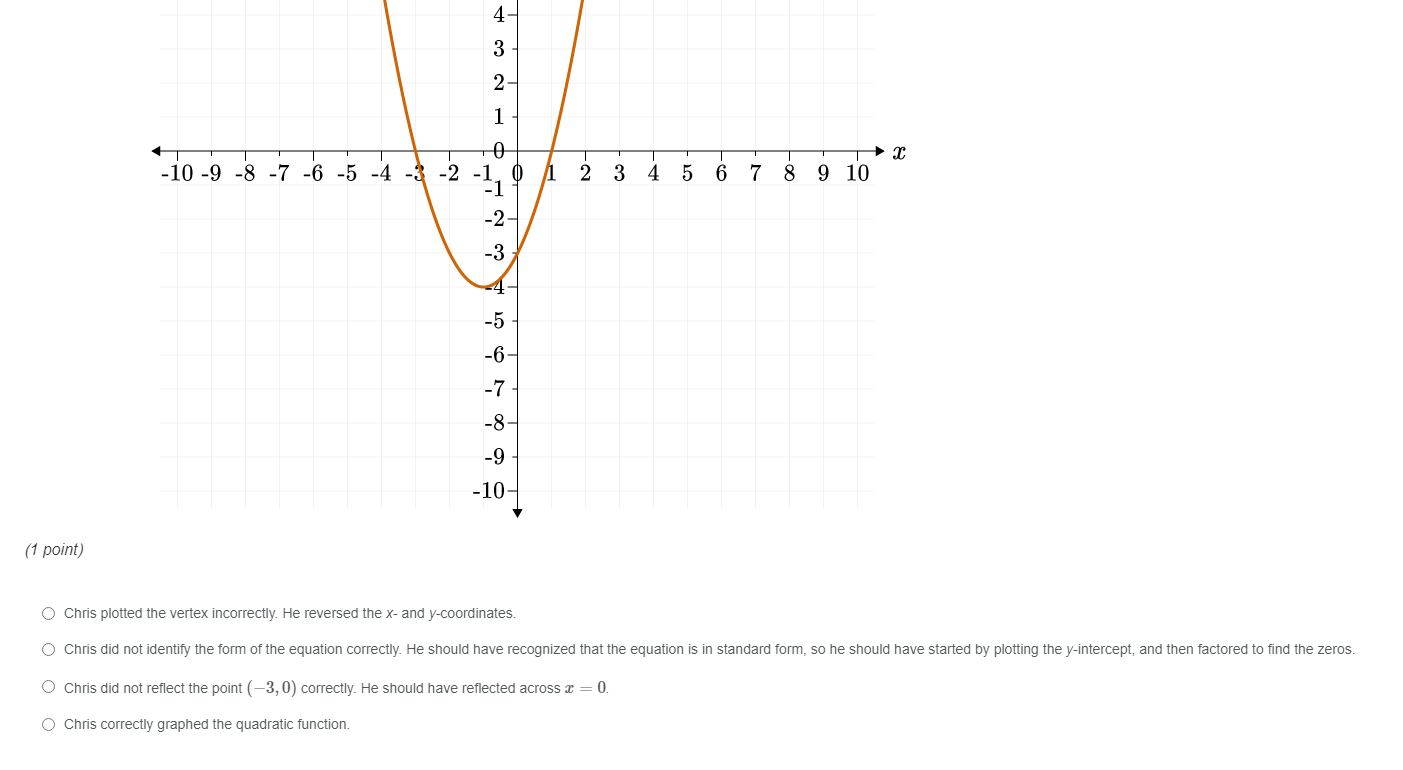


Solved Chris Is Asked To Graph The Quadratic Function F Chegg Com



3 Which Of The Following Is The Graph Of X 2 2 Y 1 2 Brainly Com



Misc 15 Find Area X Y Y2 4x 4x2 4y2 9 Miscellaneous



Solved The Graph Of Equation X 2 Xy Y 2 9 Is A Slan Chegg Com
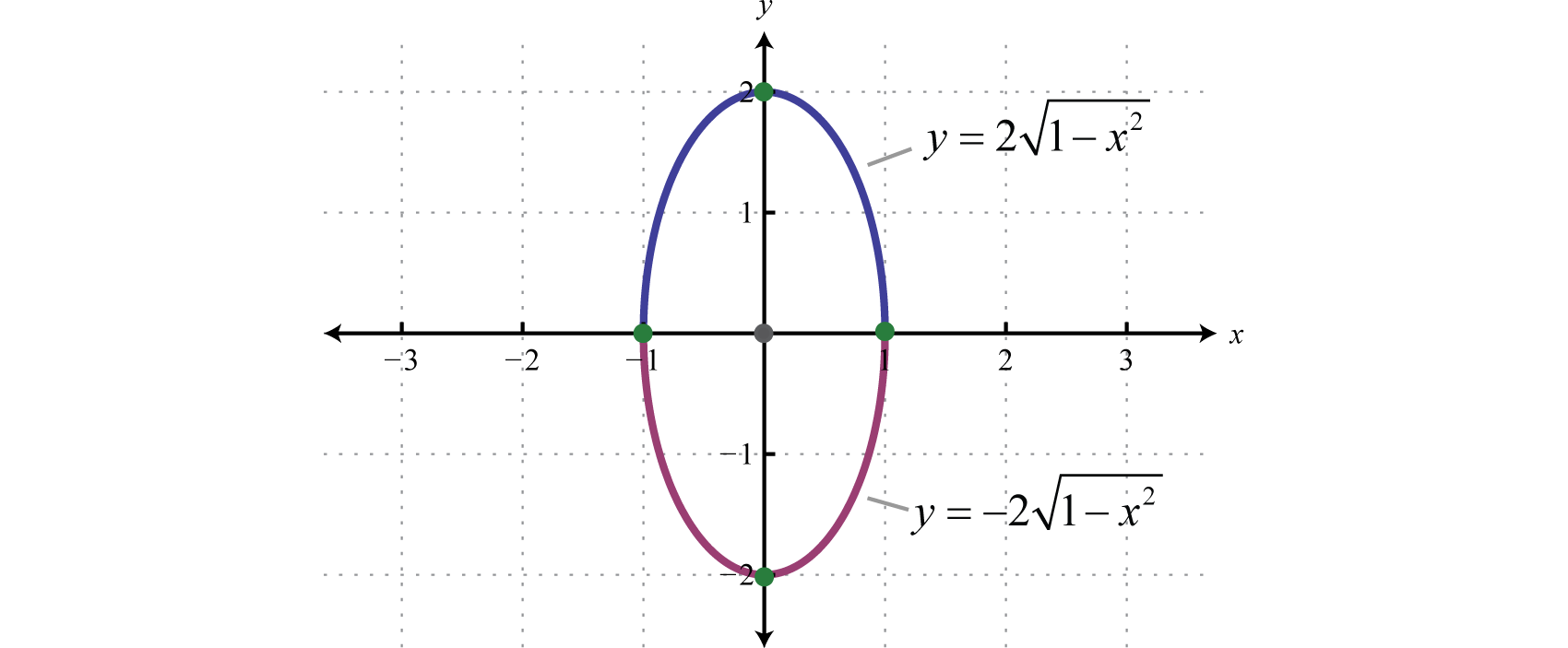


Ellipses



Assignment Previewer Http Www Webassign Net V4cgi Pages 1 19 Flip Pdf Download Fliphtml5


Pplato Basic Mathematics Quadratic Functions And Their Graphs



Graph By Plotting Points



What Is The Graph Of The Equation X 8 2 Y 1 2 9 Brainly Com



How Do You Find The Volume Of A Solid Where X 2 Y 2 Z 2 9 Is Bounded In Between The Two Planes Z 2x 2 And Z 2x 3 Socratic



Finding Inverse Functions Quadratic Example 2 Video Khan Academy



A Graph Of X 2 Y 2 9 Is Shown On The Grid By Drawing The Line X Y 2 Solve The Equations X 2 Brainly Com


How Do You Find The Area Between F X X 2 2x 1 G X 3x 3 Socratic
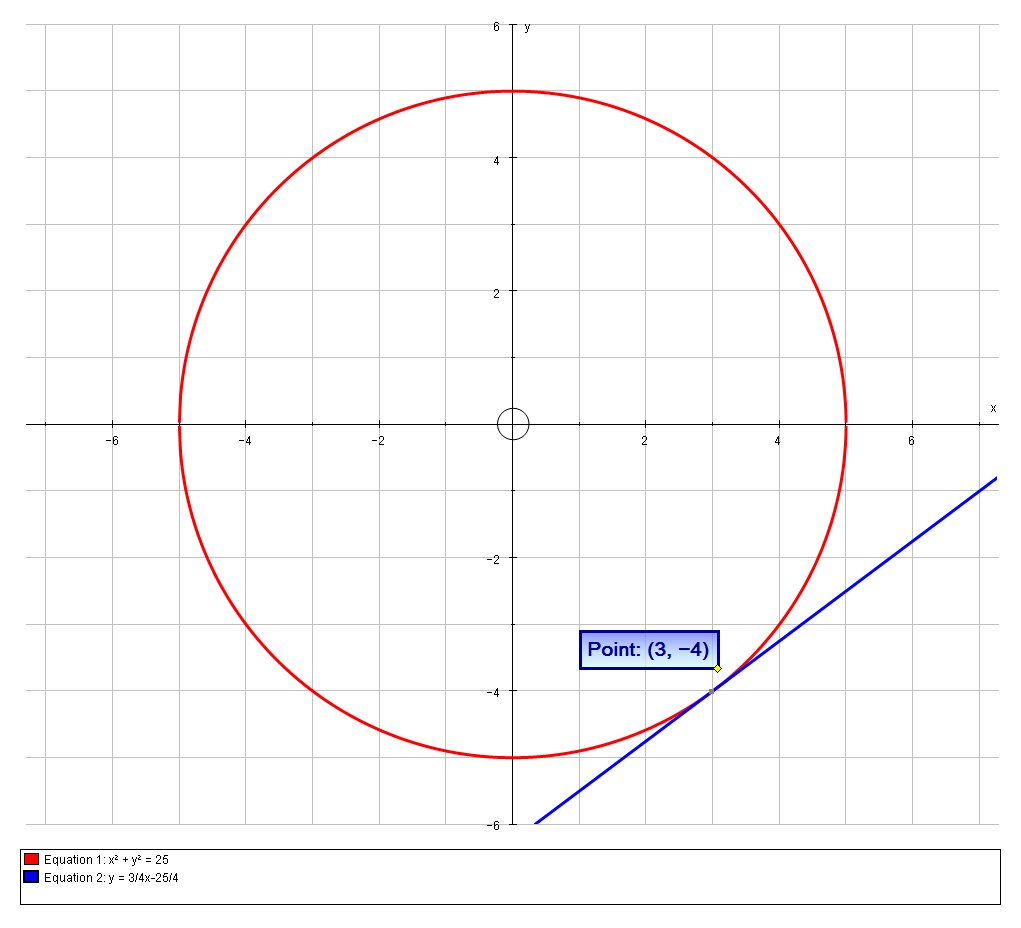


How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic


Instantcert Credit College Algebra Lesson 11



Find Domain And Range Of Function Y 1 X 2 Youtube
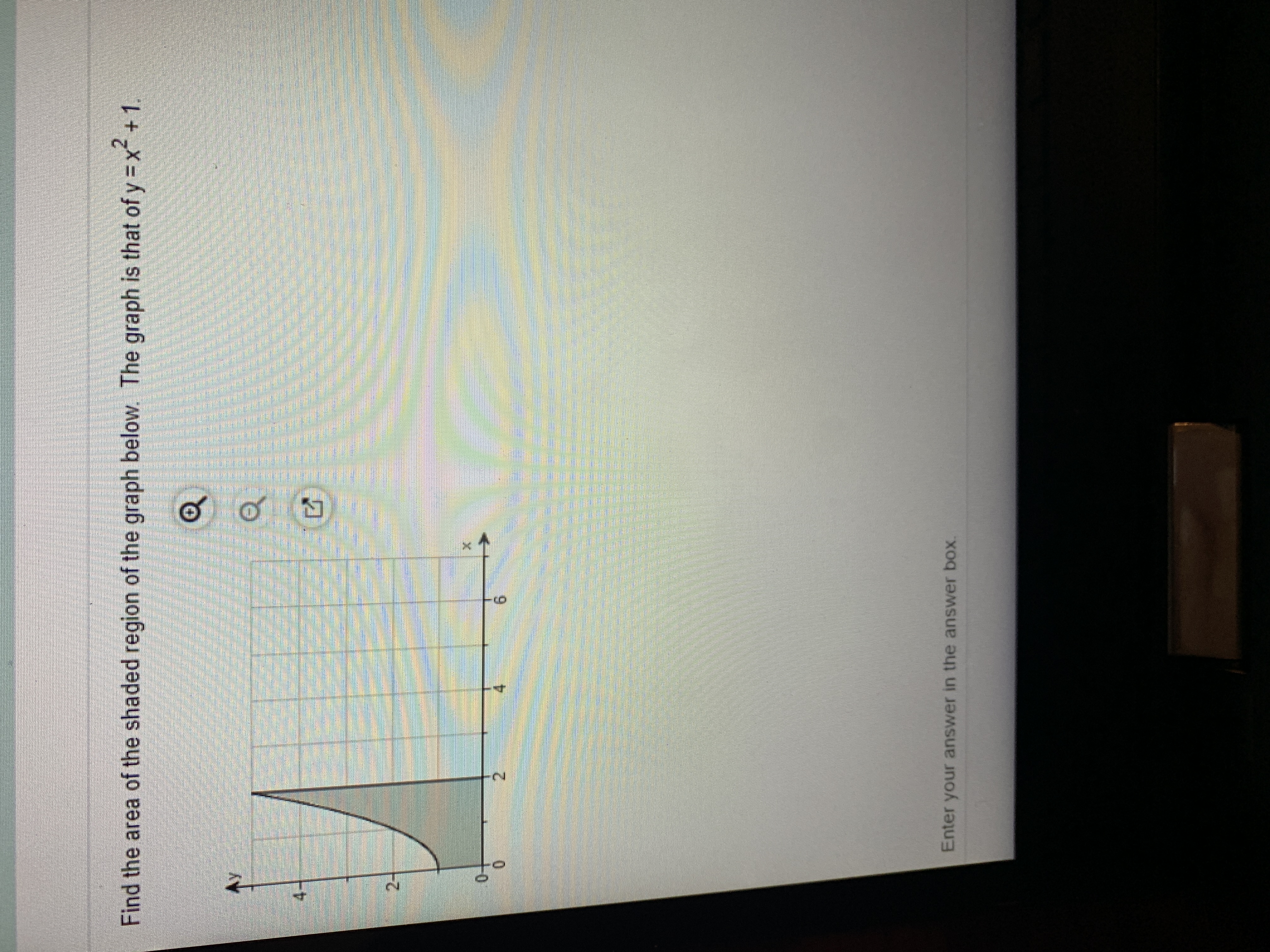


Answered Find The Area Of The Shaded Region Of Bartleby



10 3 Circles Hubarth Algebra Ii Ppt Download
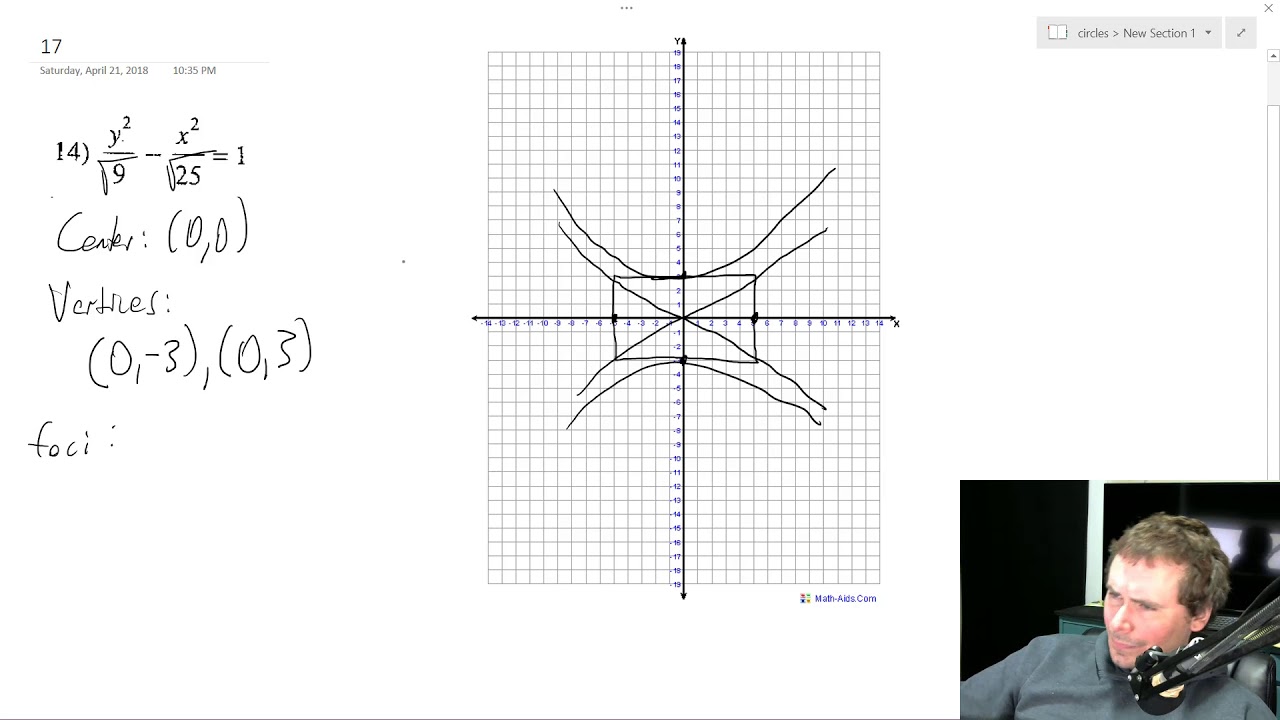


Find The Vertices Of Foci Of Y 2 9 X 2 25 1 Youtube



Solved 12 10 Points Graph 36 X 1 2 9 Y 2 2 14 Chegg Com
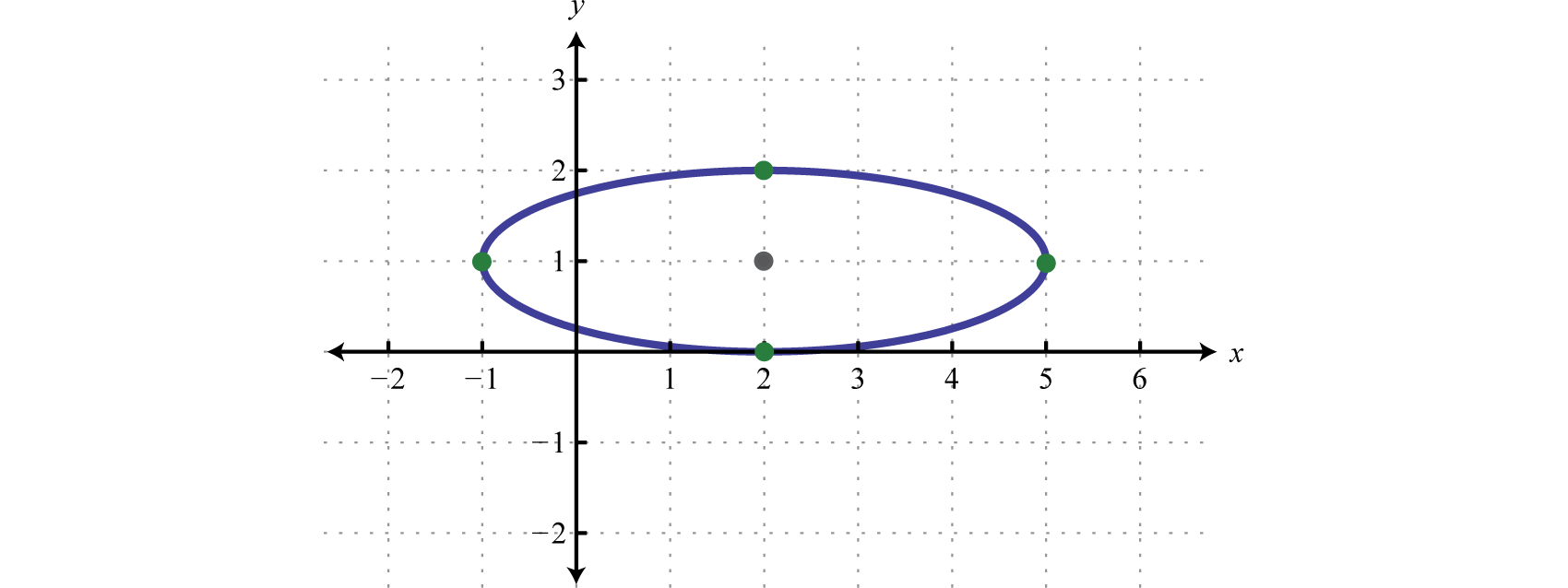


Ellipses
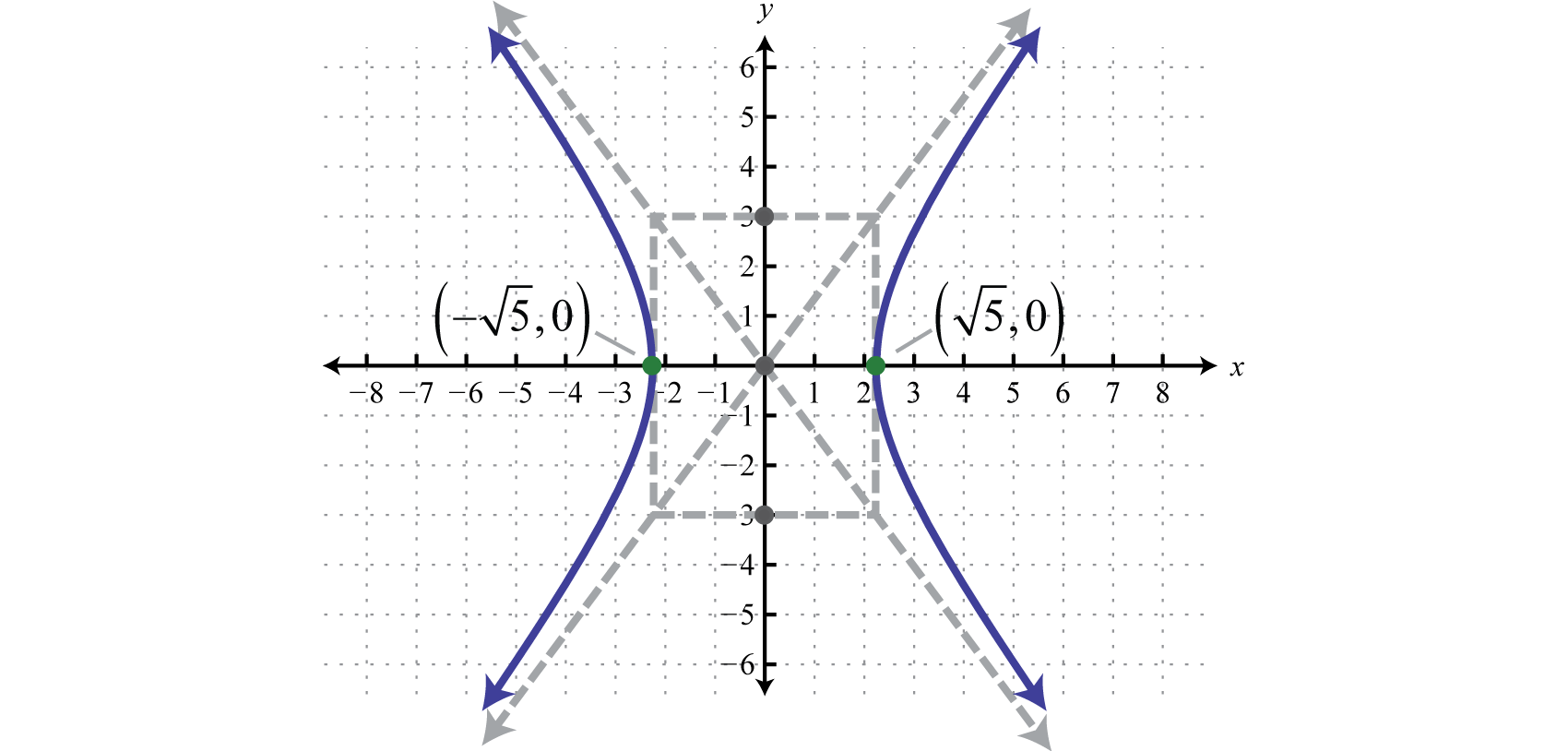


Hyperbolas



Draw The Graph Of Followings I Y X 2 Ii Y X 1 2



Sketch The Graph Of The Following Functions Y F X And Find The
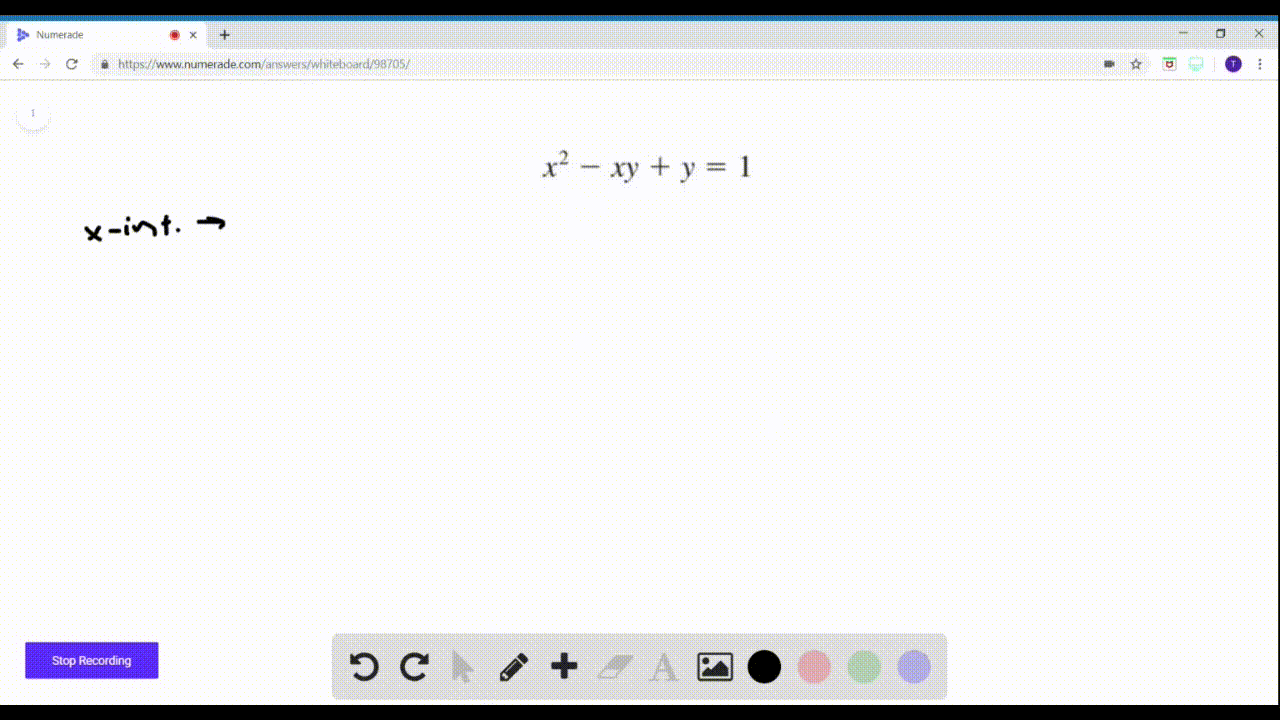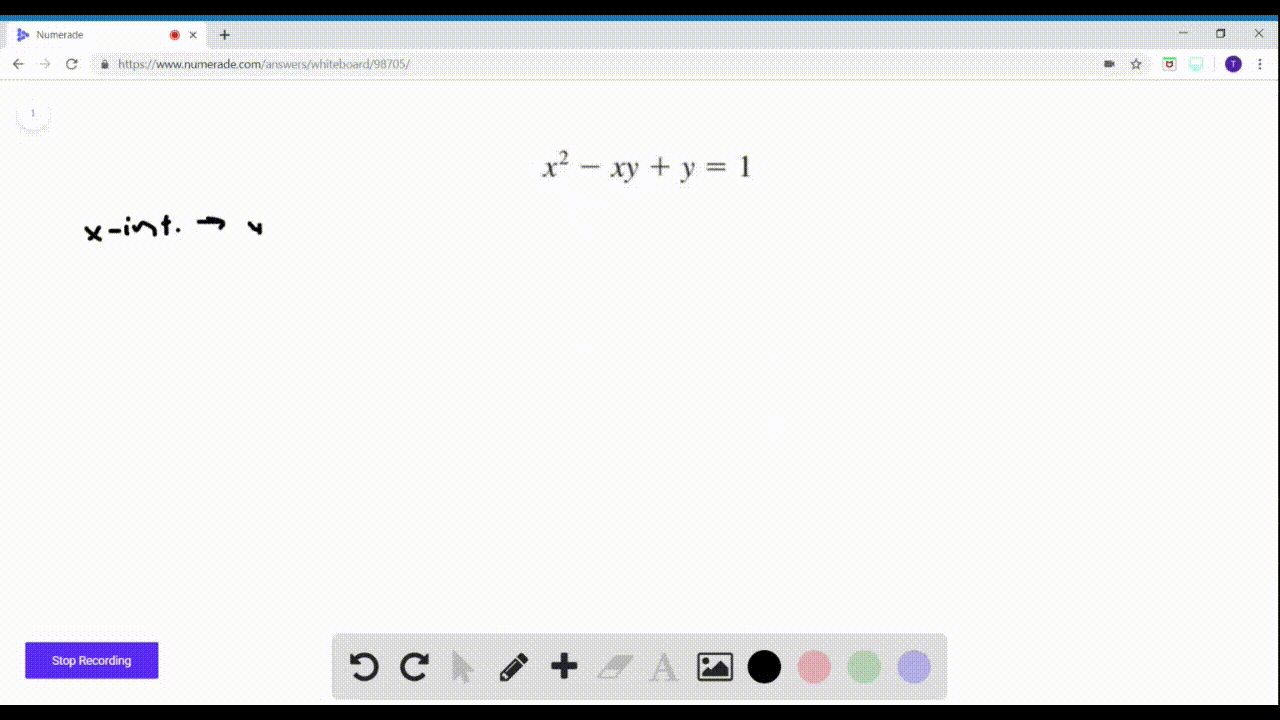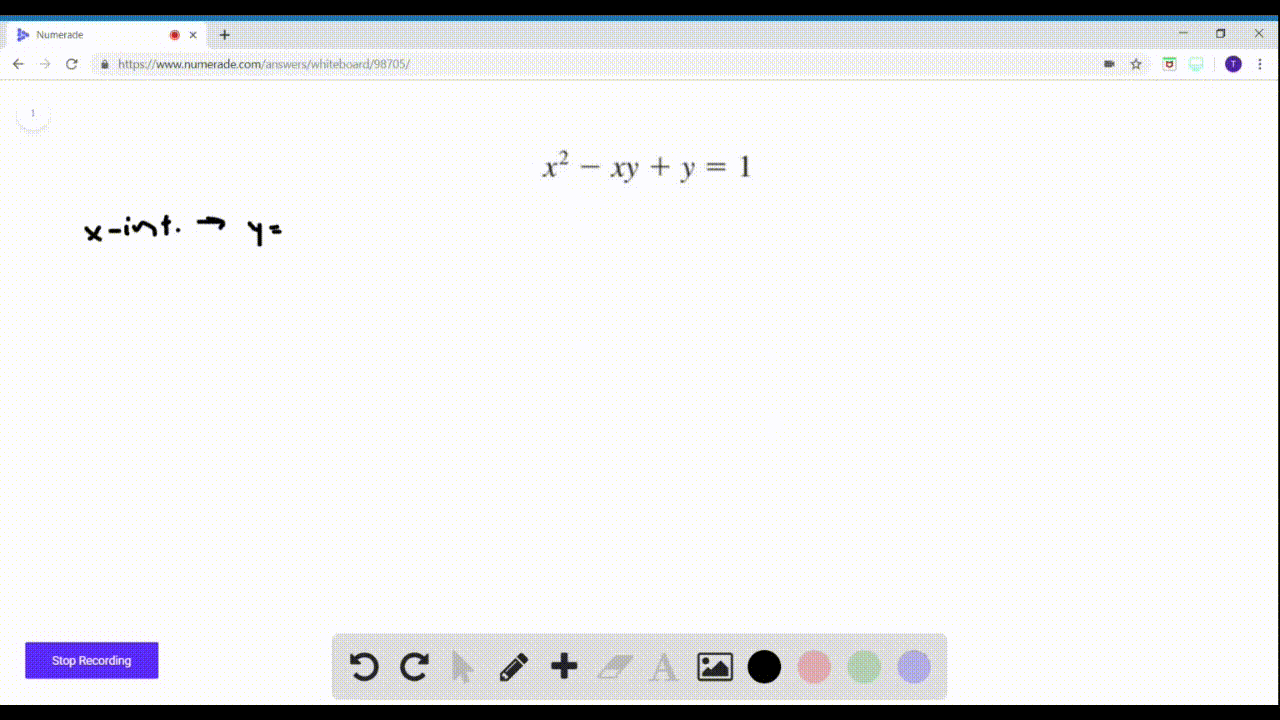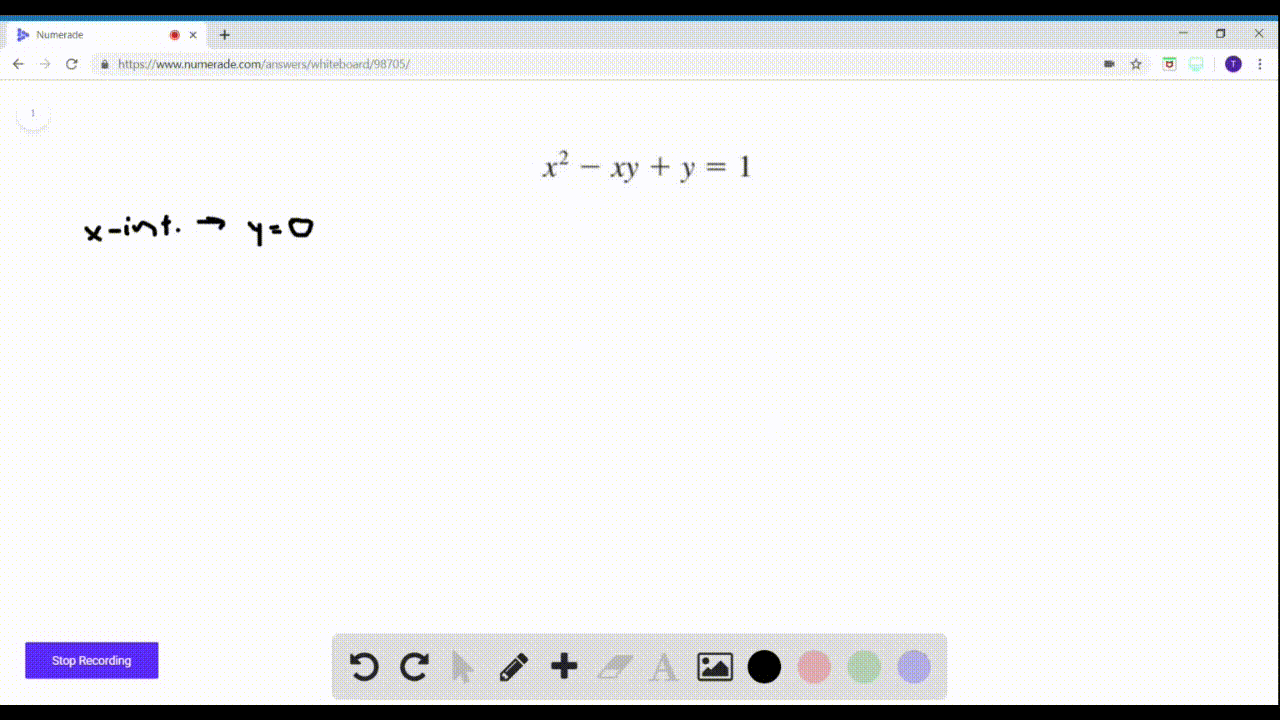


Solved 47 56 Intercepts Find The X And Y Inte
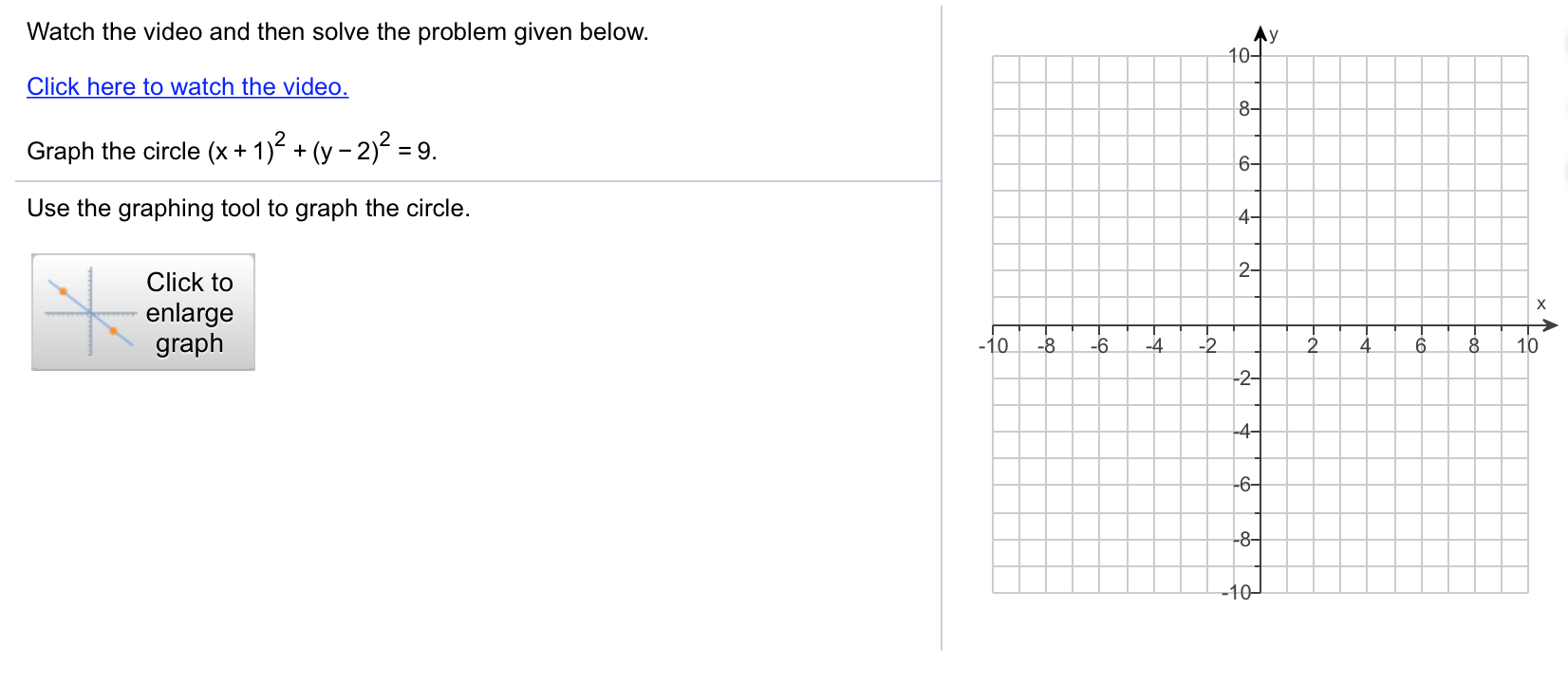


Answered Watch The Video And Then Solve The Bartleby



Solved 47 Give The Center And Radius Of The Circle Descri Chegg Com
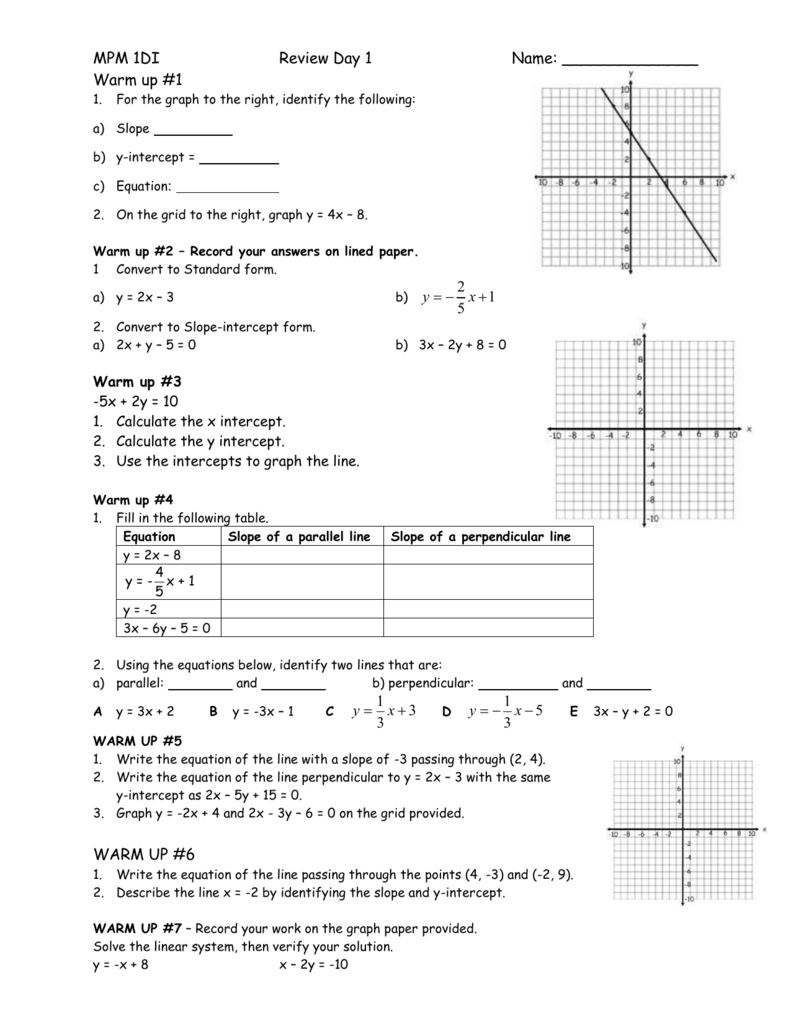


Warm Up
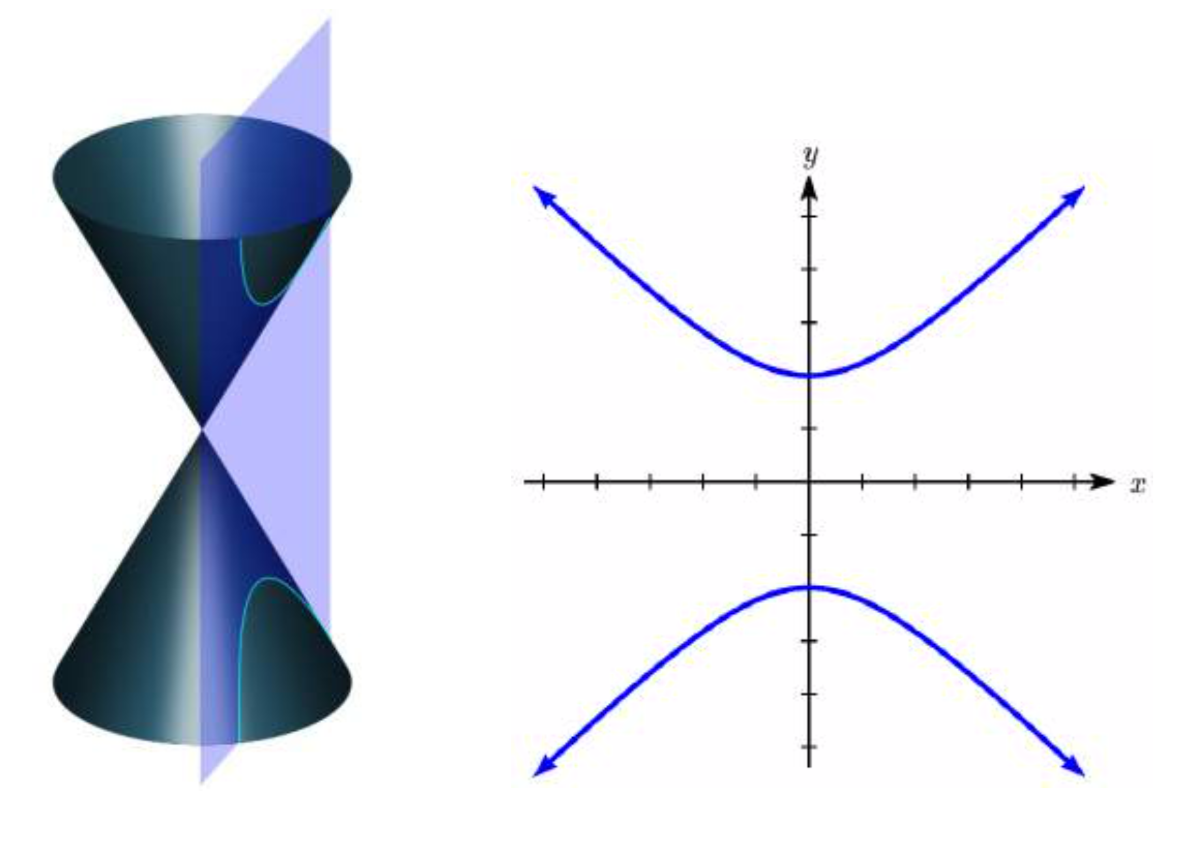


9 2 Hyperbolas Mathematics Libretexts



Find The Area Of The Region Bounded By The Curves Y Sqrt X Y X 6 And The X Axis By Integral With Respect To X Mathematics Stack Exchange



Graph Of F X X 2 X 1 Youtube
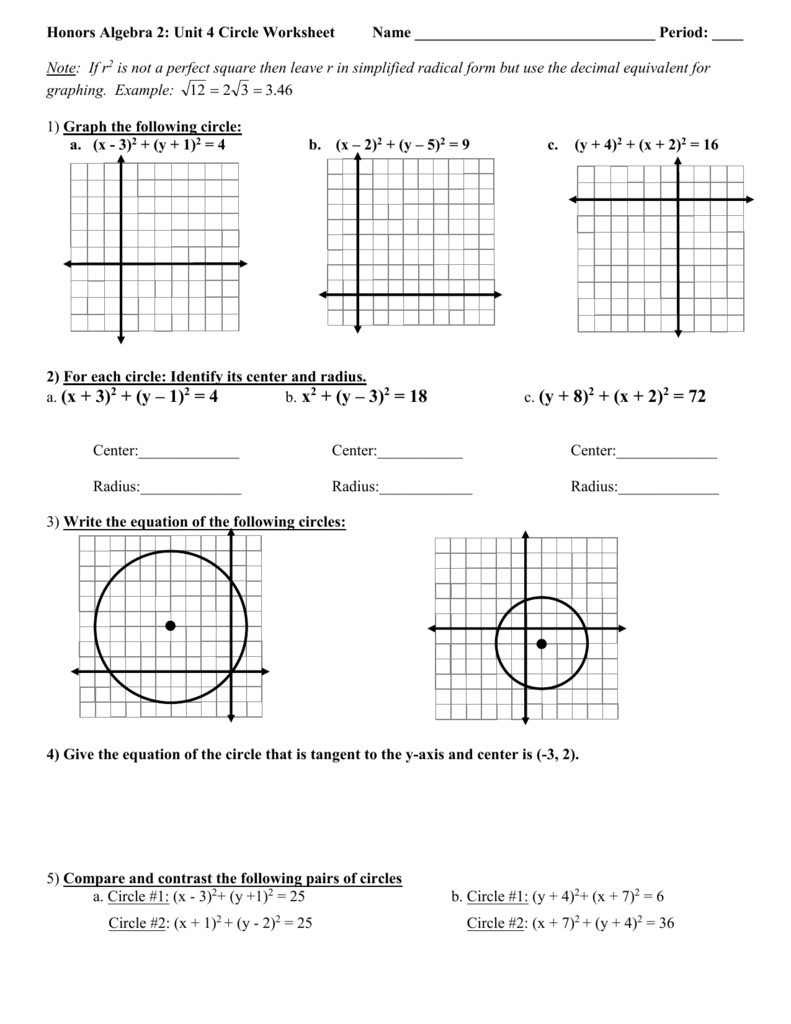


2



No comments:
Post a Comment